Representational Similarity - From Neuroscience to Deep Learning… and back again
Published:
In today’s blog post we discuss Representational Similarity Analysis (RSA), how it might improve our understanding of the brain as well as recent efforts by Samy Bengio’s and Geoffrey Hinton’s group to systematically study representations in Deep Learning architectures. So let’s get started!
What is this Representational Similarity Thing?
The brain processes sensory information in a distributed and hierarchical fashion. The visual cortex (the most studied object in neuroscience) for example sequentially extracts low-to-high level features. Photoreceptors by the way of bipolar + ganglion cells project to the lateral geniculate nucleus (LGN). From there on a cascade of computational stages sets in. Throughout the different stages of the ventral (“what” vs dorsal - “how”/”where”) visual stream (V1 $\to$ V2 $\to$ V4 $\to$ IT) the activity patterns become more and more tuned towards the task of object recognition. While neuronal tuning in V1 is mostly associated with rough edges and lines, IT demonstrates more abstract conceptual representational power. This modulatory hierarchy has been a big inspiration to the field of computer vision and the development of Convolutional Neural Networks (CNNs).
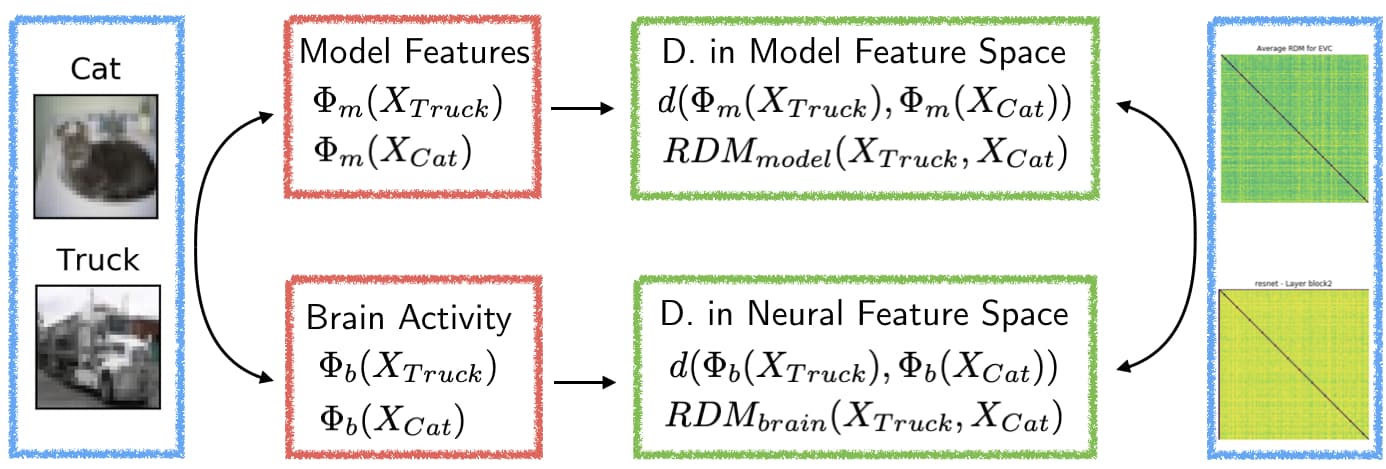
In the neurosciences, on the other hand, there has been a long lasting history of spatial filter bank models (Sobel, etc.) which have been used to study activation patterns in the visual cortex. Until recently, these have been the state-of-the-art models of visual perception. This was mainly due to the fact that the computational model had to be somehow compared to brain recordings. Therefore, the model space to investigate was severely restricted. Enter: RSA. RSA was first introduced by Kriegeskorte et al. (2008) to bring together the cognitive and computational neuroscience community. It provides a simple framework to compare different activation patterns (not necessarily in the visual cortex; see figure below). More specifically, fMRI voxel-based GLM estimates or multi-unit recordings can be compared between different conditions (e.g. the stimulus presentation of a cat and a truck). These activation measures are then represented as vectors $\Phi_b$ and we can compute distance measures between such vectors under different conditions, $d(\Phi_b(X_{truck}), \Phi_b(X_{cat}))$. This can be done for many different stimuli and each pair allows us to fill one entry of the so-called representational dissimilarity matrix ($RDM_{brain}$).
Since the original introduction of RSA, it has got a lot of press and many popular neuroscientists such as James DiCarlo, David Yamins, Niko Kriegeskorte and Radek Cichy have been combining RSA with Convolutional Neural Networks in order to study the ventral visual system. The beauty of this approach is that the dimensionality of the feature vector does not matter, since it is reduced to a single distance value which is then compared between different modalities (i.e. brain and model). Cadieu et al. (2014) for example claim that the CNNs are the best model of the ventral stream. In order to do so they extract features from the penultimate layer of an ImageNet-pretrained AlexNet and compare the features with multi-unit recordings of IT in two macaques. In a decoding exercise they find that the AlexNet features have more predictive power than simultaneously recorded V4 activity. Quite an amazing result. (In terms of prediction.) Another powerful study by Cichy et al. (2016) combined fMRI and MEG to study visual processing through time and space. A CNN does not know the notion of time nor tissue. A layer of artificial neurons can hardly be viewed as analogous to a layer in the neocortex. However, the authors found that sequence of extracted features mirrored the measured neural activation patterns in space (fMRI) and time (MEG).
These results are spectacular not because CNNs “are so similar” to the brain, but because of the complete opposite. CNNs are trained by minimizing a normative cost function via backprop and SGD. Convolutions are biologically implausible operations and CNNs process millions of image arrays during training. The brain, on the other hand, exploits inductive biases through genetic manipulation as well as unsupervised learning in order to detect patterns in naturalistic images. However, backprop + SGD and thousands of years of evolution seem to have come up with with similar solutions. But ultimately, we as researchers are interested in understanding the causal mechanisms underlying the dynamics of the brain and deep architectures. How much can RSA help us with that?
What can RSA Tell Us About the Brain?
All measures computed within RSA are correlational. The RDM entries are based on correlational distances. The $R^2$ captures the variation of the neural RDM explained by the variation in the model RDM. Ultimately, it is hard to interpret any causal insights. The claim that information in CNNs is the best model for how the visual cortex works is cheap. This really does not help a lot. CNNs are trained via backpropagation and encapsule a huge inductive bias in the form of kernel weight sharing across all neurons involved in a single processing layer. But the brain cannot implement these exact algorithmic details (and has probably found smarter solutions than Leibniz’s chain rule). However, there has been a bunch of recent work (e.g. by Blake Richards, Walter Senn, Tim Lillicrap, Richard Naud and others) to explore the capability of neural circuits to approximate a normative-gradient-driven cost function optimization. So ultimately, we might not be that far off.
Until then, I firmly believe that one has to combine RSA with the scientific method of experimental intervention. As in economics, we are in the need for quasi-experimental causality by the means of controlled manipulation. And that is exactly what has been done two recent studies by Bashivan et al. (2019) and Ponce et al. (2019)! More specifically, they use generative procedures based on Deep Learning to generate a set of stimuli. The ultimate goal thereby is to provide a form of neural control (i.e. drive firing rates of specific neural sites). Specifically, Ponce et al. (2019) show how to close the loop between generating a stimulus from a Generative Adversarial Network, reading out neural activity and altering the input noise to the GAN in order to drive the activity of single units as well as populations. The authors were able to identify replicable abstract tuning behavior of the recording sites. The biggest strength of using flexible function approximations lies in their capability to articulate patterns which we as experimenters are not able to put in words.
What can RSA Tell Us About Deep Learning?
For many Deep Learning architectures weight initialization is crucial for successful learning. Furthermore, we still don’t really understand inter-layer repesentational differences. RSA provides an efficient and easy-to-compute quantity that can measure robustness to such hyperparameters. At the last NeuRIPS conference Sami Bengio’s group (Morcos et al., 2018) introduced projected weighted canonical correlation analysis (PWCCA) to study differences in generalization as well as narrow and wide networks. Based on a large Google-style empirical analysis the came up with the following key insights:
- Networks which are capable of generalization converge to more similar representations. Intuitively, overfitting can be achieved in many different ways. The network is essentially “under-constrained” by the training data and can do whatever it wants outside of that part of the space. Generalization requires to exploit patterns related to the true underlying data-generating process. And this can only be done by a more restricted set of architecture configurations.
- The width of a network is directly related to the representational convergence. More width = More similar representations (across networks). The authors argue that this is evidence for the so-called lottery ticket hypothesis: Empirically it has been shown that wide-and-pruned networks perform a lot better than networks that were shallow from the beginning. This might be due to different sub-networks of the large-width network being initialized differently. The pruning procedure then is able to simply identify the sub-configuration with optimal initialization while the shallow network only has a single initialization from the get-go.
- Different initializations and learning rates can lead to distinct clusters of representational solutions. The clusters generalize similarly well. This might indicate that the loss surface has multiple qualitatively indistinguishable local minima. What ultimately drives the membership could not be identified yet.
A recent extension by Geoffrey Hinton’s Google Brain group (Kornblith et al., 2019) uses centered kernel alignment (CKA) in order to scale CCA to larger vector dimensions (numbers of artificial neurons). Personally, I really enjoy this work since computational models give us scientists the freedom to to turn all the nobs. And there are quite a few in DL (architecture, initialization, learning rate, optimizer, regularizers). Networks are white boxes like Kriegeskorte says. So if we can’t succeed in understanding the dynamics of a simple Multi-Layer Perceptron, how are we ever going to succeed in the brain?
Conclusion
All in all, I am a huge fan of every scientific development trying to shine some light on approximations of Deep Learning in the brain. However, Deep Learning is not a causal model of computation in the brain. Arguing that the brain as well as CNNs perform similar sequential operations in time and space is a limited conclusion. In order to gain true insights, the loop has to be closed. Using generative models to design stimuli is therefore an exciting new endeavor in neuroscience. But if we want to understand the dynamics of learning, we have to go further than that. How are loss functions and gradients represented? How does the brain overcome the necessity of requiring to separate training and prediction phases? Representations are only a very indirect peephole to answering these fundamental questions. Going forward I there is a lot to gain (from the modeler’s perspective) from skip and recurrent connections as well as Bayesian DL via dropout sampling. But that is the story of another blog post.
References
- Kriegeskorte, N., M. Mur, and P. A. Bandettini. (2008): “Representational similarity analysis-connecting the branches of systems neuroscience,” Frontiers in systems neuroscience, 2, 4.
- Cichy, R. M., D. Pantazis, and A. Oliva. (2014): “Resolving human object recognition in space and time,” Nature neuroscience, 17, 455.
- Cichy, R. M., A. Khosla, D. Pantazis, A. Torralba, and A. Oliva. (2016): “Comparison of deep neural networks to spatio-temporal cortical dynamics of human visual object recognition reveals hierarchical correspondence,” Scientific reports, 6, 27755.
- Bashivan, P., K. Kar, and J. J. DiCarlo. (2019): “Neural population control via deep image synthesis.,” Science (New York, N.Y.), 364.
- Cadieu, C. F., H. Hong, D. L. K. Yamins, N. Pinto, D. Ardila, E. A. Solomon, N. J. Majaj, and J. J. DiCarlo. (2014): “Deep Neural Networks Rival the Representation of Primate IT Cortex for Core Visual Object Recognition,” PLOS Computational Biology, 10, 1–18.
- Kornblith, S., M. Norouzi, H. Lee, and G. Hinton. (2019): “Similarity of neural network representations revisited,” arXiv preprint arXiv:1905.00414, .
- Morcos, A., M. Raghu, and S. Bengio. (2018): “Insights on Representational Similarity in Neural Networks with Canonical Correlation,” Advances in Neural Information Processing Systems, .
- Ponce, C. R., W. Xiao, P. F. Schade, T. S. Hartmann, G. Kreiman, and M. S. Livingstone. (2019): “Evolving images for visual neurons using a deep generative network reveals coding principles and neuronal preferences,” Cell, 177, 999–1009.