Automatic Differentiation (AD) is one of the driving forces behind the success story of Deep Learning. It allows us to efficiently calculate gradient evaluations for our favorite composed functions. TensorFlow, PyTorch and all predecessors make use of AD. Along stochastic approximation techniques such as SGD (and all its variants) these gradients refine the parameters of our favorite network architectures.

Many people (until recently including myself) believe that backpropagation, the chain rule and automatic differentiation are synonymous. But they are not. In order to become true masters of the craft we have to work out why. (Man these emojis are addictive).

TL;DR: We discuss different ways of differentiating computer programs. More specifically, we compare forward mode and reverse mode (backprop) automatic differentiation. Ultimately, we implement forward mode AD with dual dual numbers for a simple logistic regression problem. The plain numpy code can be found here.

Calculating Derivatives of A Computer Program

The term “differentiable programming” can be a bit mind-boggling. In general programs do not have anything to do with analysis or differentiable functions. Except for computer functions that evaluate mathematical functions. Imagine you are faced with the task of fitting some logistic regression model. One way to do so is by iteratively minimizing the binary cross-entropy loss of your logistic output function given some true labeled data (with $\sigma$ denoting the element-wise sigmoid activation function $\sigma(h) = (1+ e^{-h})^{-1})$:

The analytic expression can easily be translated into some Python code:

def binary_cross_entropy(y_true, y_pred):
    y_true = np.append(1 - y_true, y_true, axis=1)
    y_pred = np.append(1 - y_pred, y_pred, axis=1)
    bce = -(y_true * np.log(y_pred)).sum(axis=1)
    return bce

The function computes a numerical value based on the fixed true labels (y_true) and the predicted/fitted label probabilities (y_pred). In our case y_pred amounts to the sigmoid-squashed output $\sigma(X \beta)$ which is again a function of $\beta$. In order to find the best fitting $\beta$ coefficients, we need to follow the steepest descent direction (aka the gradient) that minimizes $arg\min_{\beta} \mathcal{L} \circ \sigma (X, y, \beta)$. In order to do so we have access to a set of differentiation techniques:

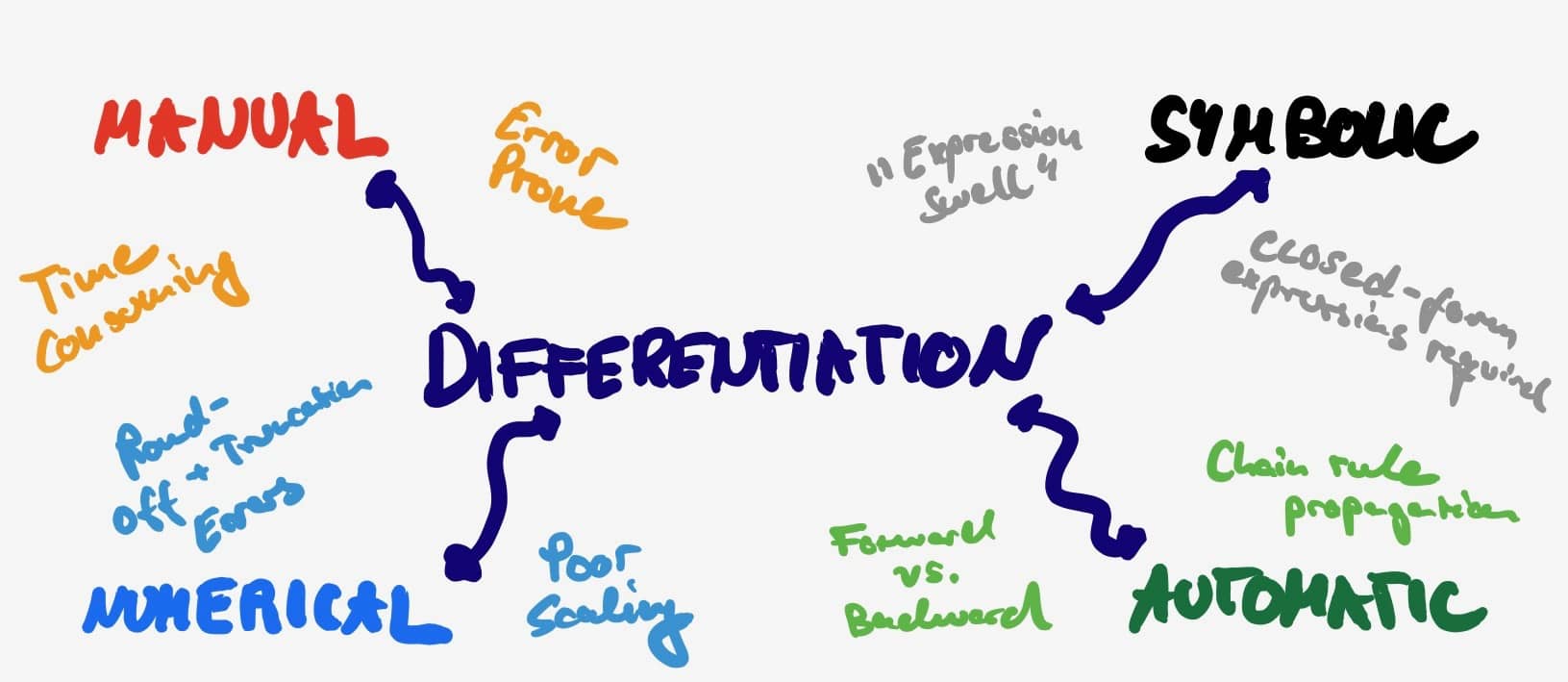
1. Manual differentiation (): As one can already tell, manual differentiation requires one to work out the derivative on a piece of paper. Afterwards, that derivative can be implement it in code. Doing so is prone to “mathy” errors and (at least for me) fairly time consuming. Good luck trying to work things out for a deep net.
2. Numerical differentiation (): Instead of getting your hands dirty with chain and quotient rules, one can simply try to approximate the gradient using two infinitesimal different inputs. By doing so we approximate the formal definition of the derivative. This comes with two main disadvantages: It requires multiple function evaluations (at least twice per input dimension) and is subject to round-off errors as well as truncation errors (inputs are never exactly the same). On the bright side - it is super easy to implement.
3. Symbolic differentiation (): Symbolic methods apply transformations which comply with the rules of differentiation in order to obtain an expression for the derivative. This is implemented in software such as Mathematica and relies upon some serious algebraic manipulations. Composing functions $f \circ g$ comes at the risk of leading to overly complicated symbolic representations of the derivative. This is commonly referred to “expression swelling”. Ultimately, this can result in arbitrarily expensive evaluations of the gradient.
4. Automatic differentiation (): Instead of swelling to infinity, AD simplifies the derivative expression at every possible point in time. For example after each operation! All of math can be viewed as compositions of a finite set of basic operations (addition, multiplication, exponentiation, etc.). And for such operations we already know the functional form of the derivative. By the beauty of the chain rule, we can combine these elementary derivative and reduce the complexity of the expression at the cost of memory storage.

At its core AD merges the best of both numerical and symbolic worlds. It calculates the value of a derivative with the help of the elementary rule set from symbolic differentiation. In order to overcome the swelling the symbolic expression is simplified at every stage. Simply by numerically evaluating with the results of the previous computations (or simply the input data). Hence, it does not provide an analytical expression for the derivative itself. Instead, it iteratively evaluates a gradient given data. Simply put: $f’(2) \neq f’(x) \ \forall x$.

Let’s see how this applies to our logistic regression problem & define the step-wise outputs as $a(h) = \sigma(h)$ and $h(X, \beta) = X \beta$. We can then rewrite the gradient of interest as:

The expression above is the manual derivation. On first sight this might not really look like a simplification. But we can now observe a more general principle: The gradient can be decomposed into gradient components of the individual transformation path:

1. Pre-activations $h(X, \beta)$ and their gradient $\nabla_\beta h(X, \beta)$ wrt the parameters.
2. Activations $a(h)$ and their gradient $\nabla_{h} a(h)$ wrt the pre-activations.
3. Log of class probs $\log a(h)$ and the gradient diagonal matrix $\nabla_a \log a(h)$.

For each of the partial evaluations $h(X, \beta), a(h), \log a(h)$ we can easily compute the sensitivity to their respective inputs $\beta, h, a$ and obtain their derivatives. Ultimately, the true probability vector $p$ provides the error signal which scales the gradient.

AD (): Forward () vs Reverse Mode ()

We can proceed to automatically compute the individual components of the gradient in two different ways:

1. Forward Accumulative Mode (): Simply put forward mode applies Leibniz’s chain rule to each basic operation in a forward primal trace. Thereby, one obtains a derivative trace. At every stage we evaluate the operator as well as its gradient in “lockstep”!
   • Primal trace: $h(X, \beta) \to a(h) \to \log a(h)$
   • Derivative trace: $\nabla_\beta h(X, \beta) \to \nabla_{h} a(h) \to \nabla_a \log a(h)$
   • Lockstep evaluation + derivative: \(h(X, \beta), \nabla_\beta h(X, \beta) \to a(h), \nabla_{h} a(h), \to \log a(h), \nabla_a \log a(h)\) Finally, the overall gradient $\nabla_\beta \mathcal{L}$ is then obtained by multiplying the individual pieces together and rescaling with $p$.
2. Reverse Accumulative Mode (): Reverse mode, on the other hand, does not compute derivatives simultaneously but requires two separate phases. During a forward phase all intermediate variables are evaluated and their values stored in memory. In a following backward phase we then propagates back the derivatives/adjoints with the help of again the chain rule. Reverse mode AD is what we commonly refer to as backpropagation (Rumelhart et al., 1988) in Deep Learning.
   • Forward phase: $h(X, \beta) \to a(h) \to \log a(h)$
   • Backward phase: $\nabla_a \log a(h) \to \nabla_h a(h) \to \nabla_\beta h(X, \beta)$ So how do we know in which way to send our gradient? We need a bookkeeping scheme which is provided by the pre-specified computational graph that specifies the flow of operations.

There are two main considerations when comparing the modes of operation:

1. Memory Storage vs Time of Computation: Forward mode requires us to store the derivatives, while reverse mode AD only requires storage of the activations. While forward mode AD computes the derivative at the same time as the variable evaluation, backprop does so in the separate backward phase.
2. Input vs Output Dimensionality: Given a function $f: \mathbb{R}^n \to \mathbb{R}^m$ we can differentiate between two regimes based on the dimensions to be processed:
   • $n « m$: The input dimension is smaller than the output. The operations applied expand the dimensionality from a set of few units. $\Rightarrow$ Forward mode is computationally cheaper than reverse mode.
   • $n » m$: The input dimension is larger than the output. This is the classical Deep Learning setting. We obtain a scalar loss evaluation from a forward pass and propagate back to a fairly high-dimensional input. $\Rightarrow$ Reverse mode is computationally cheaper than forward mode.

We are interested in pushing computations from a few units towards many. Things are not necessarily this clear cut since one can fairly easily vectorize the forward mode computations. Hence, no separate forward passes are required. I assume that reverse mode’s dominance in DL results mainly from the reduced memory requirements.

The Role of Dual Numbers

So here comes an algebraic magic trick that simplifies forward mode AD: It can be shown that forward mode AD is equivalent to evaluating the function of interest with dual numbers.

My motivation for this blog post stemmed from being unsatisfied with my understanding of exactly this equivalence. So I had to dig a little deeper. Let me now try to shine some light onto the elegance of using the dual part of any numerical evaluation to calculate its respective parameter gradients. So what are dual numbers again? We can decompose the input variable $x$ into a real and into a dual part:

with $v, \dot v \in \mathbb{R}$, $\epsilon \neq 0$ and $\epsilon^2 = 0$. Based on this simple definition the following basic arithmetic properties result:

Furthermore, one can algebraically derive the following:

Wow! By evaluating $f(x)$ in its dual form and setting $\dot v = 1$ we are able to recover both the function value $f(v)$ as well as its evaluated derivative $f’(v)$ in the form of the coefficient in front of $\epsilon$! Finally, the chain rule smoothly translates into the dual setting:

This means that we can easily propagate gradients across the layers of computation simply be multiplying derivatives with each other. To implement the dual numbers we simply require a separate storage systems that keeps track of $x = (v, \text{ coeff in front of }\dot v)$ & apply the respective derivative computations to the dual part of $x$. Awesome algebra!

For multivariate functions things become a little trickier. Imagine two inputs:

The partial derivative with respect to $x$ is computed by setting $v=1$ and $u=0$. For $y$ we have to flip both bits. In order to do so in parallel and to prevent several forward passes, we can vectorize things and keep a diagonal matrix: \(\left(\begin{array}{cc} 1 & 0\\ 0 & 1 \end{array}\right)\) with each row representing one partial derivative. All of the above rules then easily translate into the multivariate case.

So it remains to discuss how to think about $\epsilon$? Two intuition which I stole from this blog post are the following:

1. $\epsilon$ can be thought of as a form of infinitesimal number. When squaring such a small number it simply becomes non-representable. Intuitively, this is similar to the numerical differentiation step size.

2. Another possible way to think of $\epsilon$ is as a matrix: \(\left(\begin{array}{cc} 0 & 1\\ 0 & 0 \end{array}\right)\). Computing $\epsilon \times \epsilon$ then yields the required null matrix.

By restricting $i^2 = -1$ imaginary numbers, help us in computing rotations. Dual numbers, on the other hand, restrict $\epsilon^2 = 0$ and allow for efficient and exact derivative evaluation. Let’s see how we can translate this into code for our logistic regression example.

Let’s Code it Up!

First, we need some synthetic data for our binary classification problem. The class object below generates coefficients, Gaussian noise and features. Afterwards, we take the dot-product and threshold the transformed features in order to obtain the binary labels. Furthermore, there are some small utilities in order to sample batches of data and to shuffle the data between epochs. All pretty standard stuff. Nothing dual.

class DataLoader(object):
    # Small class object for generating synthetic data
    def __init__(self, n, d, batch_size, binary=False):
        self.total_dim = d + 1
        self.X, self.y = self.generate_regression_data(n, d, binary)
        # Set batch_id for different indices
        self.num_batches = np.ceil(n/batch_size).astype(int)
        self.batch_ids = np.array([np.repeat(i, batch_size) for i in range(self.num_batches)]).flatten()[:n]

    def generate_regression_data(self, n, d, binary=False):
        # Generate the regression/classification data from Gaussians
        self.b_true = self.generate_coefficients(d)
        X = np.random.normal(0, 1, n*d).reshape((n, d))
        noise = np.random.normal(0, 1, n).reshape((n, 1))
        inter = np.ones(n).reshape((n, 1))
        X = np.hstack((inter, X))
        y = np.matmul(X, self.b_true) + noise
        # Make data binary if task is classification/logistic regression
        if binary:
            y[y > 0] = 1
            y[y <= 0] = 0
        return X, y

    def generate_coefficients(self, d, intercept=True):
        # Generate random integer-valued coefficients for Xb + e
        b_random = np.random.randint(-5, 5, d + intercept)
        return b_random.reshape((d + intercept, 1))

    def shuffle_arrays(self):
        # Shuffle the dataset for diversity when looping over batches
        assert len(self.X) == len(self.y)
        p = np.random.permutation(len(self.X))
        self.X, self.y = self.X[p], self.y[p]

    def get_batch_idx(self, batch_id):
        # Subselect the current batch to be processed!
        idx = np.where(self.batch_ids == batch_id)[0]
        return self.X[idx, :], self.y[idx].flatten()

Next let’s define the “dual meat” of things. We need to make sure that all of our elementary operations (addition, multiplication, the sigmoid activation as well as the log needed for the gradient) act on the real as well as dual part of the dual representation of a vector (that requires a gradient). Hence, we need a dual wrapper and to overload/redefine the operators.

class DualTensor(object):
    # Class object for dual representation of a tensor/matrix/vector
    def __init__(self, real, dual):
        self.real = real
        self.dual = dual

    def zero_grad(self):
        # Reset the gradient for the next batch evaluation
        dual_part = np.zeros((len(self.real), len(self.real)))
        np.fill_diagonal(dual_part, 1)
        self.dual = dual_part
        return

def dot_product(b_dual, x, both_require_grad=False):
    # Function to perform dot product between a dual and a no grad_req vector
    real_part = np.dot(x.real, b_dual.real)
    dual_part = np.dot(x.real, b_dual.dual)
    if both_require_grad:
         dual_part += np.dot(b_dual.real, x.dual)
    return DualTensor(real_part, dual_part)

def add_duals(dual_a, dual_b):
    # Operator non-"overload": Add a two dual numbers
    real_part = dual_a.real + dual_b.real
    dual_part = dual_a.dual + dual_b.dual
    return DualTensor(real_part, dual_part)

def log(dual_tensor):
    # Operator non-"overload": Log (real) & its derivative (dual)
    real_part = np.log(dual_tensor.real)
    temp_1 = 1/dual_tensor.real
    # Fill matrix with diagonal entries of log derivative
    temp_2 = np.zeros((temp_1.shape[0], temp_1.shape[0]))
    np.fill_diagonal(temp_2, temp_1)
    dual_part = np.dot(temp_2, dual_tensor.dual)
    return DualTensor(real_part, dual_part)

def sigmoid(dual_tensor):
    # Operator non-"overload": Sigmoid (real) & its derivative (dual)
    real_part = 1/(1+np.exp(-dual_tensor.real))
    temp_1 = np.multiply(real_part, 1-real_part)
    # Fill matrix with diagonal entries of sigmoid derivative
    temp_2 = np.zeros((temp_1.shape[0], temp_1.shape[0]))
    np.fill_diagonal(temp_2, temp_1)
    dual_part = np.dot(temp_2, dual_tensor.dual)
    return DualTensor(real_part, dual_part)

The dual-version of the sigmoid function applies the standard $\sigma(.)$ to the real part and changes the numerical value of the dual matrix of dimension $n_{batch} \times d$ with its evaluated derivative. Since $\sigma’(h) = \sigma(h) (1 - \sigma(h))$ is applied to each element of the vector $h$. Hence, the overall change to the dual part is given by:

Which results again in a Jacobian of size $n_{batch} \times d$. Same notion carries over to the log operator. Now that we got the arithmetic settings redefined for our dual number operations, let’s investigate how we can obtain our logistic regression predictions and the corresponding binary cross-entropy loss:

def forward(X, b_dual):
    # Apply element-wise sigmoid activation
    y_pred_1 = sigmoid(dot_product(b_dual, X))
    y_pred_2 = DualTensor(1-y_pred_1.real, -y_pred_1.dual)
    # Make numerically stable!
    y_pred_1.real = np.clip(y_pred_1.real, 1e-15, 1-1e-15)
    y_pred_2.real = np.clip(y_pred_2.real, 1e-15, 1-1e-15)
    return y_pred_1, y_pred_2

def binary_cross_entropy_dual(y_true, y_pred_1, y_pred_2):
    # Compute actual binary cross-entropy term
    log_y_pred_1, log_y_pred_2 = log(y_pred_1), log(y_pred_2)
    bce_l1, bce_l2 = dot_product(log_y_pred_1, -y_true), dot_product(log_y_pred_2, -(1 - y_true))
    bce = add_duals(bce_l1, bce_l2)
    # Calculate the batch classification accuracy
    acc = (y_true == (y_pred_1.real > 0.5)).sum()/y_true.shape[0]
    return bce, acc

Finally, lets put everything together in a final training loop. We generate the binary data and initialize some placeholder lists to store our intermediate results. Afterwards, we compute the Sklearn solution coefficients to measure how far we are off. Then we can simply loop over the individual batches. We initialize the coefficients as a dual tensor, sample batches, set the gradient coefficients/diagonal matrix back to their partial derivative initialization. We obtain predictions and the loss. The dual of the loss evaluation corresponds to the gradient of interest $\nabla_\beta \mathcal{L}$. SGD updates then simply take the dual and perform a step in the steepest descent direction.

def train_logistic_regression(n, d, n_epoch, batch_size, b_init, l_rate):
    # Generate the data for a coefficient vector & init progress tracker!
    data_loader = DataLoader(n, d, batch_size, binary=True)
    b_hist, func_val_hist, param_error, acc_hist = [], [], [], []

    # Get the coefficients as solution to optimized sklearn function
    logreg = LogisticRegression(penalty='none', solver='lbfgs', multi_class='multinomial')
    logreg.fit(data_loader.X, data_loader.y)
    norm_coeff = np.linalg.norm(logreg.coef_.ravel())

    # Initialize coefficient vector as a dual class instance
    b_dual = DualTensor(b_init, None)

    # Start running the training loop
    for epoch in range(n_epoch):
        # Shuffle the batch identities at beginning of each epoch
        data_loader.shuffle_arrays()
        for batch_id in range(data_loader.num_batches):
            # Clear the gradient
            b_dual.zero_grad()
            # Select the current batch & perform "mini-forward" pass
            X, y = data_loader.get_batch_idx(batch_id)
            y_pred_1, y_pred_2 = forward(X, b_dual)
            # Calculate the forward AD - real = func, dual = deriv
            current_dual, acc = binary_cross_entropy_dual(y, y_pred_1, y_pred_2)
            # Perform grad step & append results to the placeholder list
            b_dual.real -= l_rate*np.array(current_dual.dual).flatten()
            b_hist.append(b_dual.real)
            func_val_hist.append(current_dual.real)
            param_error.append(np.linalg.norm(logreg.coef_.ravel() - b_hist[-1])/norm_coeff)
            acc_hist.append(acc)

        if np.abs(param_error[-1] - param_error[-2]) < 0.00001:
            break

        if epoch % 1 == 0:
            print("Accuracy: {} | Euclidean Param Norm: {} | fct min: {}".format(acc, param_error[-1], current_dual.real))
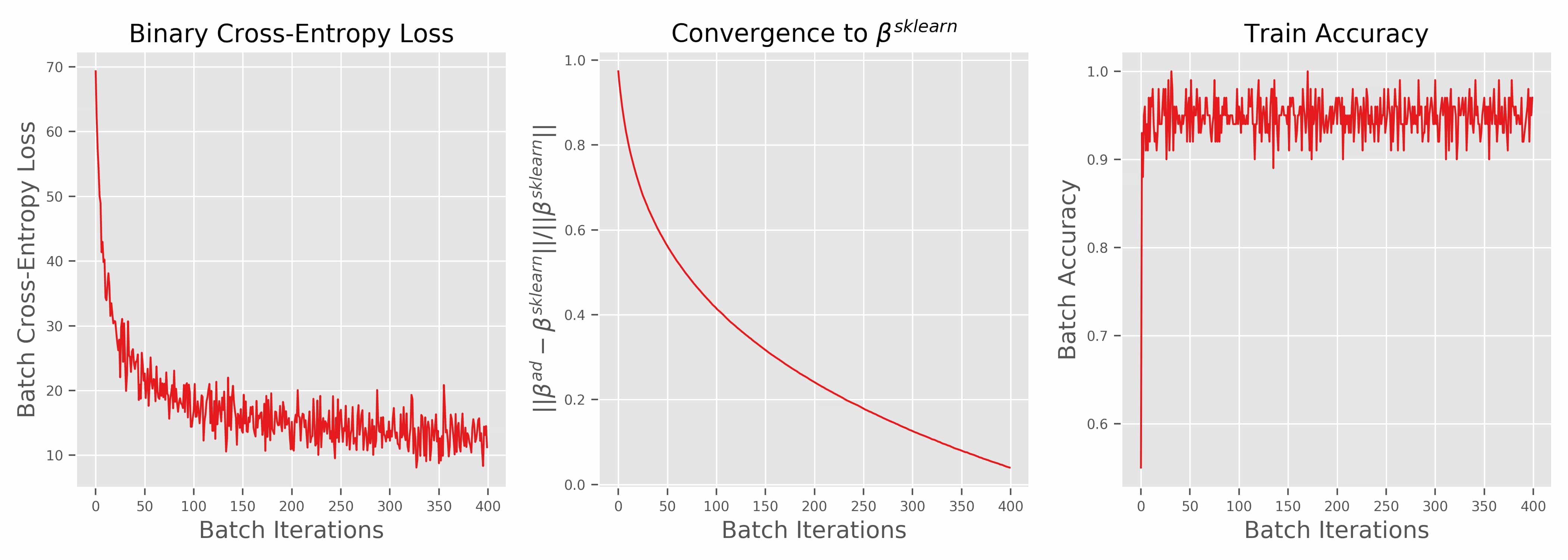
    return b_hist, func_val_hist, param_error, acc_hist

Let’s train a simple example and have a look at the metrics:

# Train a logistic regression classifier with dual number forward mode AD
b, f, e, a = train_logistic_regression(1000, 4, 40, 100,
                                       np.array([0., 0., 0., 0., 0.]),
                                       0.005)

And what a surprise the theory works out. The loss decreases with the number of batches processed. The coefficients converge to the Sklearn solution and the training accuracies sky-rockets. Hannibal from the A-Team would say “I love it when a plan comes together.”

So what? Computing Hessian-Vector Products Efficiently

We have already discussed why backpropagation and reverse mode AD are more efficient for standard Deep Learning applications. One reason why forward mode AD might still come in handy is its utility in computing Hessian-vector products, $Hv$. We can use a reverse-on-forward configuration to combine both forward and reverse mode for computing the 2nd order Hessian. More specifically, given a function $f: \mathbb{R}^n \to \mathbb{R}$ with input $x \in \mathbb{R}^n$ we can simply use both modes together:

1. Forward mode: Compute the gradient vector product $\nabla f v$ by setting $\dot x = v$.
2. Reverse mode: Take the result and apply backpropagation to it: $\nabla^2 f v = H_f v$

Smart, right? The Hessian can then be used to do higher-order optimization that also respects the approximate curvature of the loss surface. In conclusion: There is still some love left for forward mode AD.

Conclusion

We have seen the power as well as limitations of forward mode automatic differentiation. It allows us to evaluate a function and its derivative at the same time. Thereby, one is able to overcome the two phase doctrine of reverse mode AD aka backprop. This comes at the cost of storing the dual representations of all intermediate nodes. Furthermore, the computational effort of a separate backward pass is shifted to the forward pass. We saw how the magical algebraic properties of dual numbers allowed us to do so efficiently and exact.

All in all I found it extremely satisfying as well as super insightful to implement things from scratch. I think very differently about the current DL libraries as well as their challenges (e.g. static vs dynamic computational graphs, storage vs computation). I recommend the interested reader to have a closer look at a great survey by Baydin et al. (2018). The paper was my starting point and provides a very readable overview! Also you can find all the code over here.

References

1. Baydin, A. G., B. A. Pearlmutter, A. A. Radul, and J. M. Siskind. (2018): “Automatic differentiation in machine learning: a survey,” Journal of machine learning research, 18.
2. Rumelhart, D. E., G. E. Hinton, R. J. Williams, and others. (1988): “Learning representations by back-propagating errors,” Cognitive modeling, 5, 1.